Meta-learning for Likelihood-free Bayesian Optimization

This blogpost is about why we set out to write our paper “MALIBO: Meta-learning for Likelihood-free Bayesian Optimization” (📄paper, 🤖code) and provides a brief overview of its main contributions.

MALIBO: Meta-learning for Likelihood-free Bayesian Optimization

Bayesian Optimization (BO) is the tool of choice for expensive black-box optimization tasks, but its effectiveness often breaks down when dealing with high-dimensional, noisy, and heterogeneously scaled problems across diverse tasks. Traditional meta-learning BO frameworks, which are built atop Gaussian Processes (GPs), struggle with these due to their modeling assumptions and scalability limitations.

In this paper, we propose MALIBO (Meta-learning for LIkelihood-free Bayesian Optimization): meta-learning the acquisition function itself, rather than the surrogate model. It combines likelihood-free acuqisition functions with a task-uncertainty-aware meta-learning strategy, resulting in a robust and scalable optimization framework.

What is Meta-learning BO?

Bayesian optimization (BO) aims to optimize an expensive black-box function: \[\begin{equation} \mathbf x^{*} = \argmin_{\mathbf x \in \mathcal{X}} f(\mathbf{x}) \end{equation}\]

Meta-learning BO leverages information from past optimization experiences to accelerate the current optimization process.

Fig.1 - (Left) historical data from various tasks. (Right) Meta-learning model captures the information from histrical data for optimizing the target task..

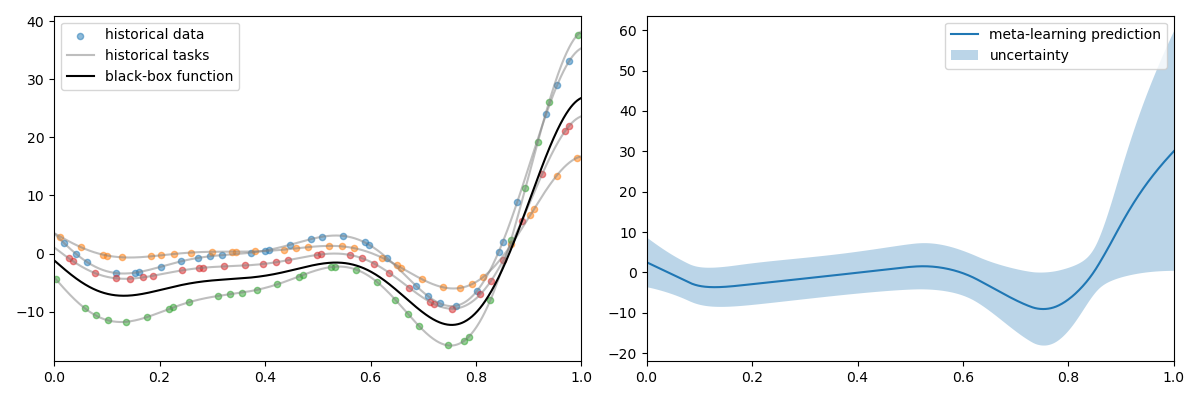
Motivation: Why Move Beyond GPs in Meta-BO?

Despite the prevalence of GPs in BO, their application in meta-learning is fraught with several limitations:

• Poor scalability in both data and task number due the cubic computational complexity.
• Sensitivity to scale mismatches across tasks (e.g., validation loss on MNIST vs. CIFAR).
• Homoscedastic Gaussian noise assumptions, often violated in real-world data.
• Deterministic task similarity models, which lead to unreliable adaptation when the target task diverges from seen distributions.

To address these, MALIBO abandons traditional surrogate modeling and instead learns a classifier-based acquisition function, which can directly infer the utility of a query without modeling the response surface.

How to tackle these limitations?

Direct approximation for acquisition function

MALIBO is based on likelihood-free Bayesian optimization (LFBO) [1], which bypasses surrogate modeling by directly approximating the acquisition function. This approach eliminates the computational bottleneck associated with GPs and imposes fewer assumptions on the target functions.

Specifically, LFBO reformulates the approximation of the acquisition function as a binary classification problem. Observed data points are labeled as “good” or “bad” based on whether they exceed a predefined threshold \(\tau\). A probabilistic classifier \(C_{\theta}(\mathbf{x})\) is then trained to estimate the probability that a given input \(\mathbf{x}\) belongs to the “good” class. This probability serves as a proxy for the acquisition function, guiding the selection of new evaluation points by maximizing the classifier’s output.

Fig.2 - (Left) A Gaussian process model and the acquisition function (Right) LFBO approximates the acquisition function directly by casting the problem into a classification problem

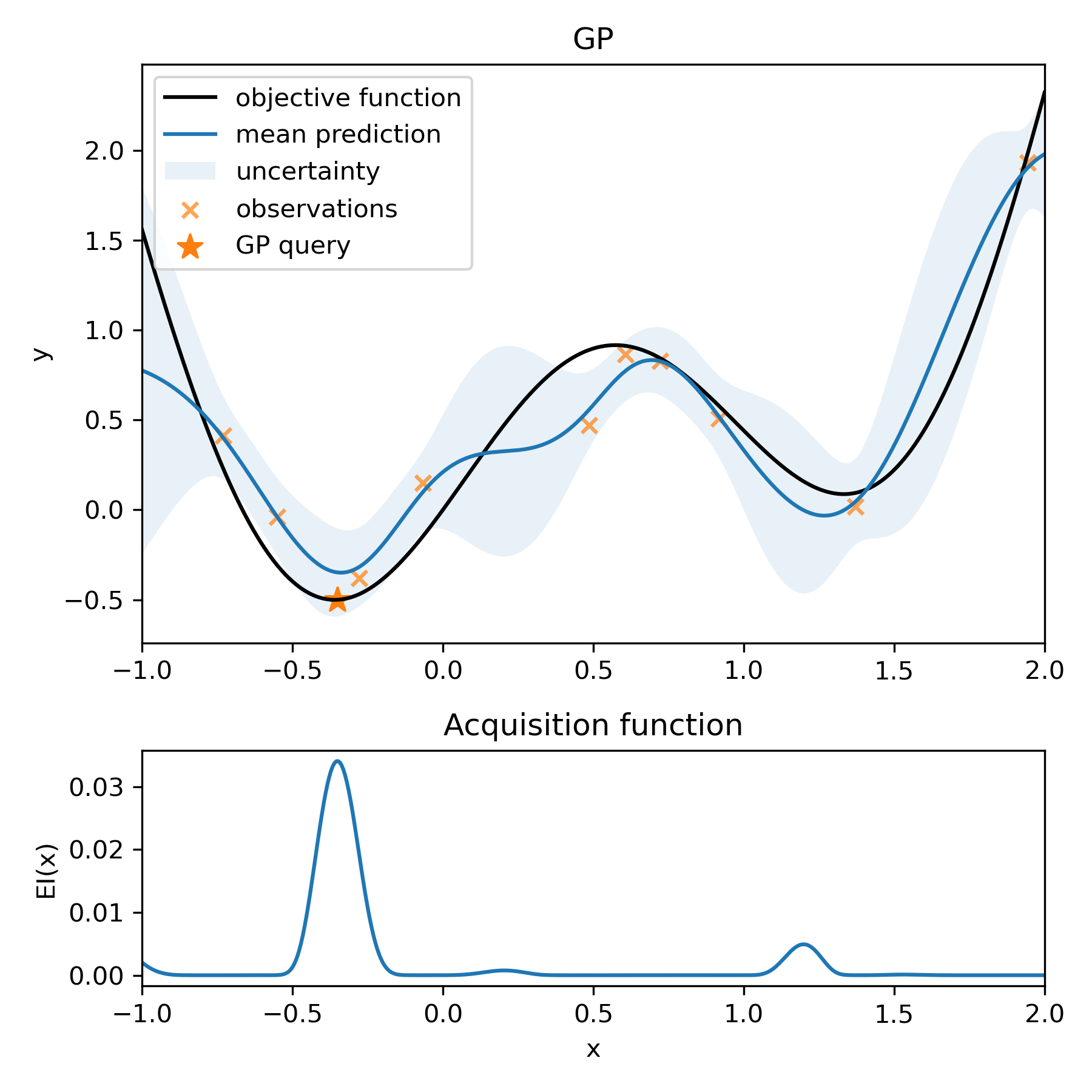
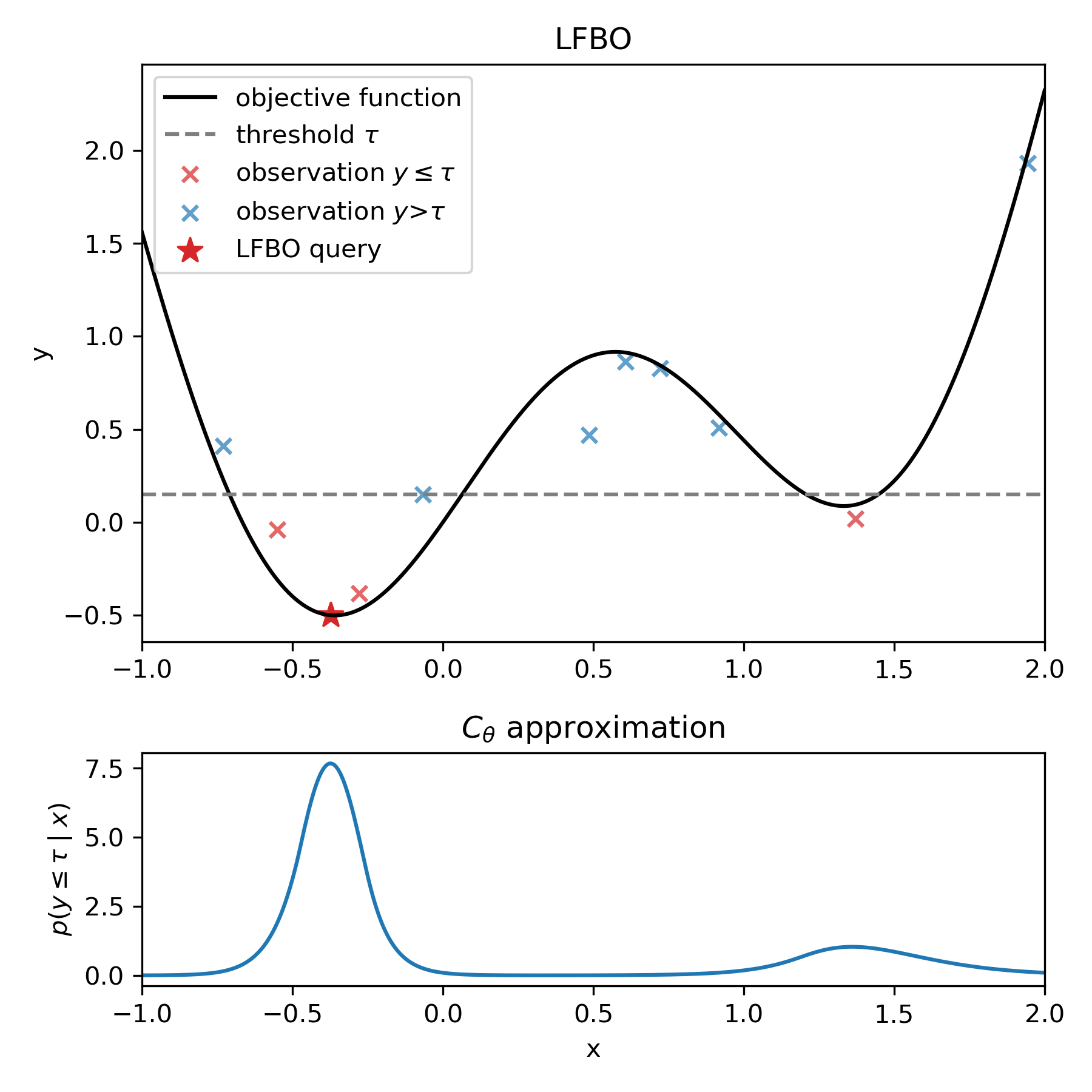
Uncertainty-awared Meta-learning

The LFBO framework enables scalable Bayesian optimization by directly approximating the acquisition function through classification, thereby avoiding strong assumptions about the black-box function or noise distribution. To extend this approach to a meta-learning setting, we require a classifier that can incorporate knowledge from prior tasks and generalize effectively to new ones. Unlike using regression model, such a meta-learning classifier is less sensitive to the heterogeneous scales in different tasks, which can improve the meta-learning performance.

Fig.3 - The classifier consists of two key components. 1. The task-agnostic part learns a shared feature mapping across all tasks, capturing the common structure and regularities that are transferable between tasks. 2. The task-specific embedding is modeled as a linear layer that modulates the shared features, introducing task-dependent variations to adapt the model to the current task. The final prediction is obtained by summing the outputs of these two components and applying a sigmoid activation, resulting in a probabilistic, binary prediction.

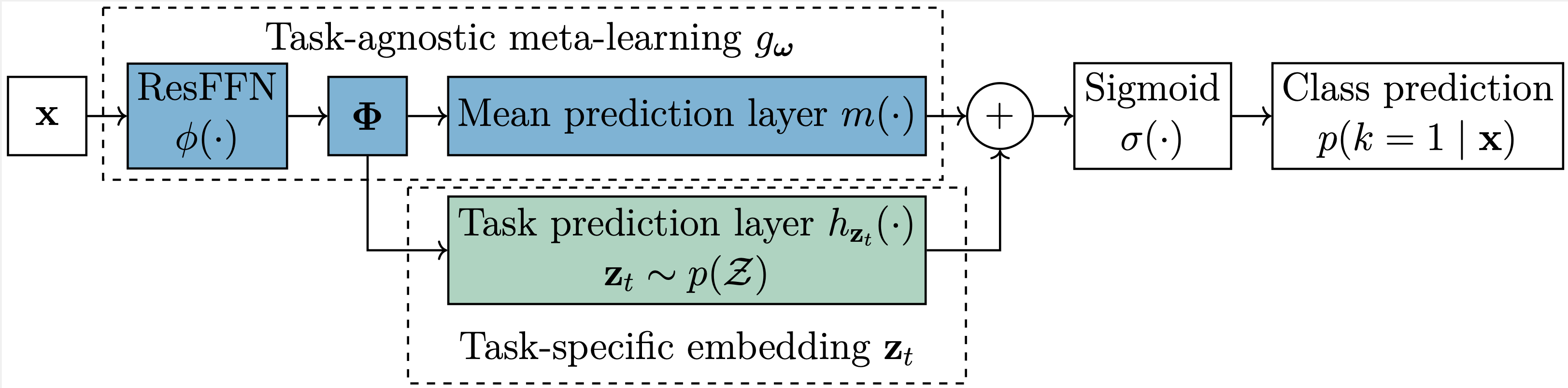
The meta-learning in MALIBO is constructed as followed: - Task-Agnostic Feature Mapping: A residual feedforward network maps input \(x\) to a shared feature space \(\phi(x)\), with a mean prediction head \(m(\phi(x))\).

• Task-Specific Latent Embeddings: Each task \(t\) is associated with an embedding (the weight in the linear layer) \(z_t \sim \mathcal{N}(0, I)\), and the classifier outputs \(C(x) = \sigma \left( m(\phi(x)) + z_t^\top \phi(x) \right)\)

With this meta-learning classifier, the model can adapt to new tasks by estimating a task-specific embedding \(z\) using the learned feature mapping. A straightforward approach would be to treat this as a maximum likelihood problem and directly optimize for \(z\) on the target task. However, this ignores task uncertainty and can lead to unreliable adaptation and over-exploitation of limited data. Moreover, when there is a mismatch between the meta-training data distribution and the non-i.i.d. data collected during optimization, a deterministic model may fail to generalize effectively. To address these issues, we adopt a Bayesian approach to task adaptation. By modeling the uncertainty in the task embedding, our classifier becomes more robust and exploratory, enabling better generalization to new and diverse tasks.

We introduce two components to mitigate these issues: a probabilistic way for meta-learning and a residual prediction module to make prediction solely based on target task.

Probabilistic training and task adaptation

• Probabilistic meta-learning: During training, the embedding \(z\) is encourage to follow a prior distribution \(\mathcal{N}(\mathbf{0}, \mathbf{I})\) in order to enable Bayesian inference during task adaptation.
• Bayesian Adaptation via Laplace Approximation: A posterior over \(z\) is inferred using Laplace approximation around the maximum-a-posteriori estimate \(q(z) \approx \mathcal{N}(z_{\text{MAP}}, \Sigma)\).
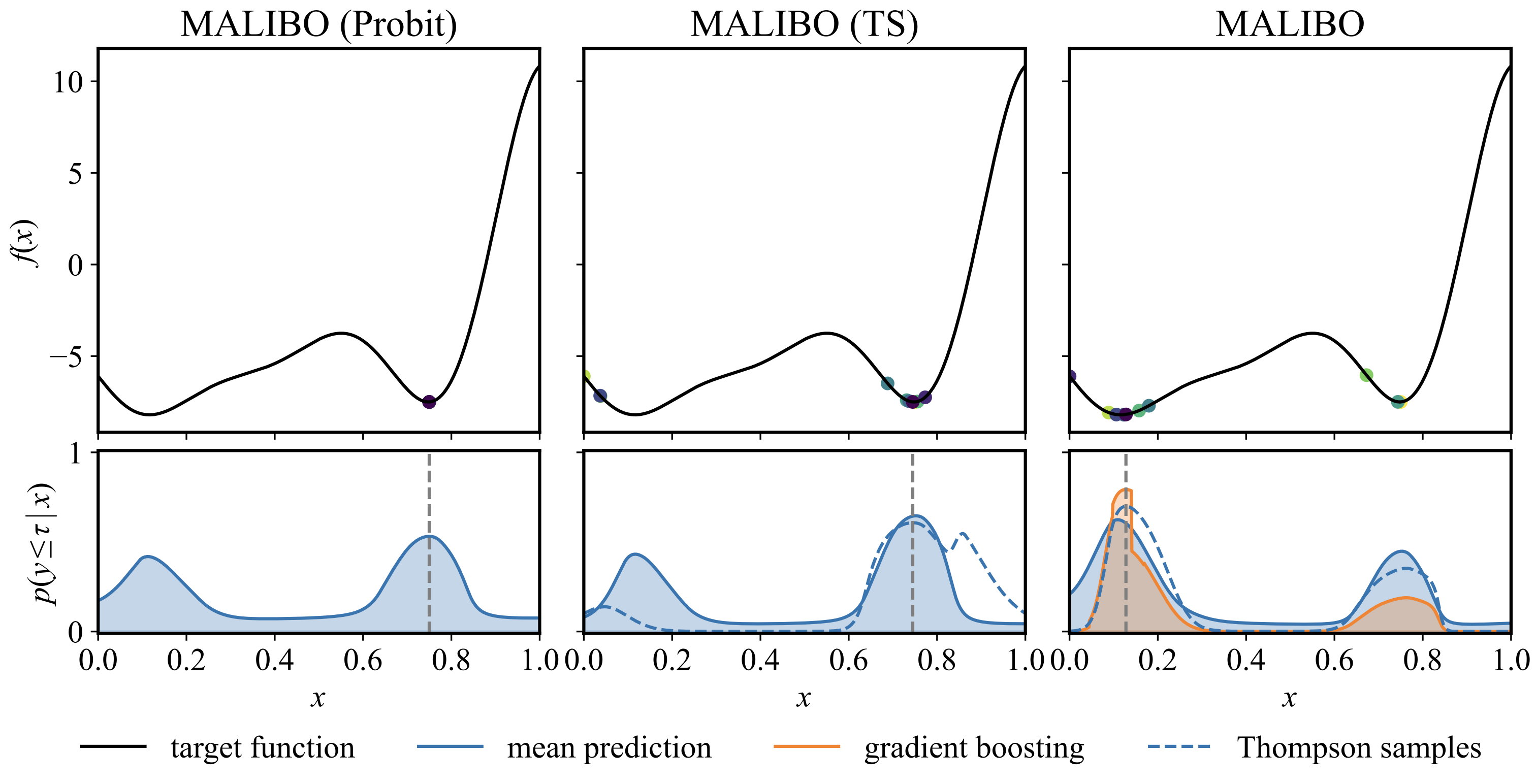
• Thompson Sampling: Enables exploratory behavior early on, and naturally supports parallel BO. Exploration is encouraged by sampling \(z \sim q(z)\) and using: \(C(x) = \sigma \left( m(\phi(x)) + h_{z}(x) \right)\)

Residual prediction module for robust adaptation

To handle out-of-distribution tasks or compensate for weak meta priors, MALIBO augments its prediction with a gradient boosting classifier trained on residuals from the meta-model.

Fig.4 - Effects of exploration and residual predictions. Color circles denote the optimization queries (from bright to dark), the dashed curve denotes a Thompson sample (TS) of the acquisition function and the orange curve shows the sample combined with gradient boosting (GB).

Results

Benchmarks: - NASBench-201: NAS with 6D discrete space, evaluated on CIFAR-10/100 and ImageNet-16. - HPOBench: 9D HPO problem on UCI datasets. - HPO-B: Large-scale HPO benchmark.

Fig.5 - Aggregated normalized regrets for BO algorithms on real-world AutoML problems.

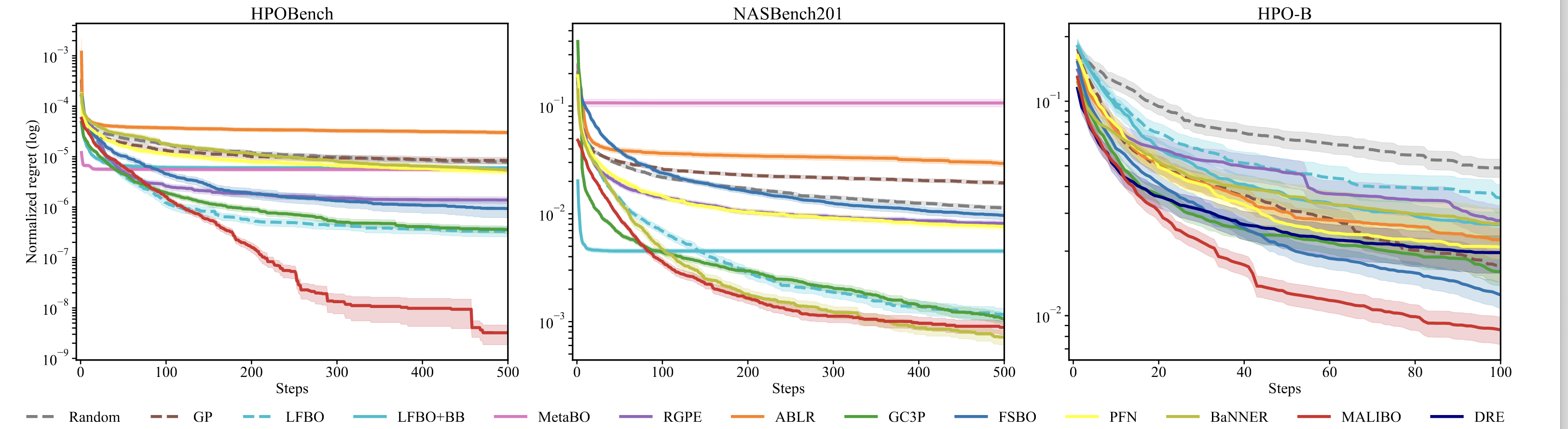
Performance: - Faster convergence and better anytime performance than GP, ABLR, MetaBO, and even LFBO. - More robust to scale shifts and heteroscedastic noise. - Low computational overhead—Thompson sampling and Laplace approximation are lightweight compared to GP training or MCMC.

References

[1] Song, Jiaming, Lantao Yu, Willie Neiswanger, and Stefano Ermon. “A General Recipe for Likelihood-Free Bayesian Optimization.”, ICML 2022