LoRA and Beyond. Fine-Tuning LLMs for Anyone, Anywhere
The Two Phases of LLM Development
The world of Large Language Models (LLMs) is scaling at an exponential rate. With training costs for base models reaching millions or even billions of dollars, the traditional method of training a model from scratch for every new task or new data is simply unsustainable. This necessity has divided the LLM development pipeline into two distinct phases: pre-training and post-training.
Pre-training: This is the initial, resource-intensive phase where the LLM learns fundamental language patterns, facts, and broad capability through a massive dataset. This results in a base model that is only capable of performing next-token prediction, generating plausible continuations of text, yet it cannot adapt its answer to the user intent.
Post-training: This phase adapts the highly capable base model for real-world deployment. The goal is to direct its broad knowledge toward specific goals. This process includes:
- Task-specific fine-tuning: The general adaptation of the base model to improve performance on new tasks, specific domains, or new data.
- Alignment: A critical refinement process that ensures the model’s responses are in the correct format, helpful and harmless. This often involves using techniques like Instruction-Tuning (IT), Reinforcement Learning from Human Feedback (RLHF) and Direct Preference Optimization (DPO).
Consider, for instance, a model that is prompted with the question What is the capital of the Netherlands?. A pre-trained model which is only capable of generating continuations of text might respond by asking another question or by providing broad information about the Netherlands rather than giving a concise answer. However, the user’s expectation in this case is a clear and direct response - Amsterdam -, and this is where post-training techniques come into play. By adapting the pre-trained model to the user intent, post-training ensures that the model provides a direct answer and only later it follows up with additional relevant context. To illustrate this difference, let’s compare the outputs of Llama-3.2-1B (base model) with Llama-3.2-1B-Instruct (instruction-tuned model).

When the prompt involves new information that the model was not exposed to during pre-training, the base model is unable to produce an accurate answer. In such cases, it often generates plausible but incorrect information, a common behavior in LLMs known as hallucination.

The Fine-Tuning Problem
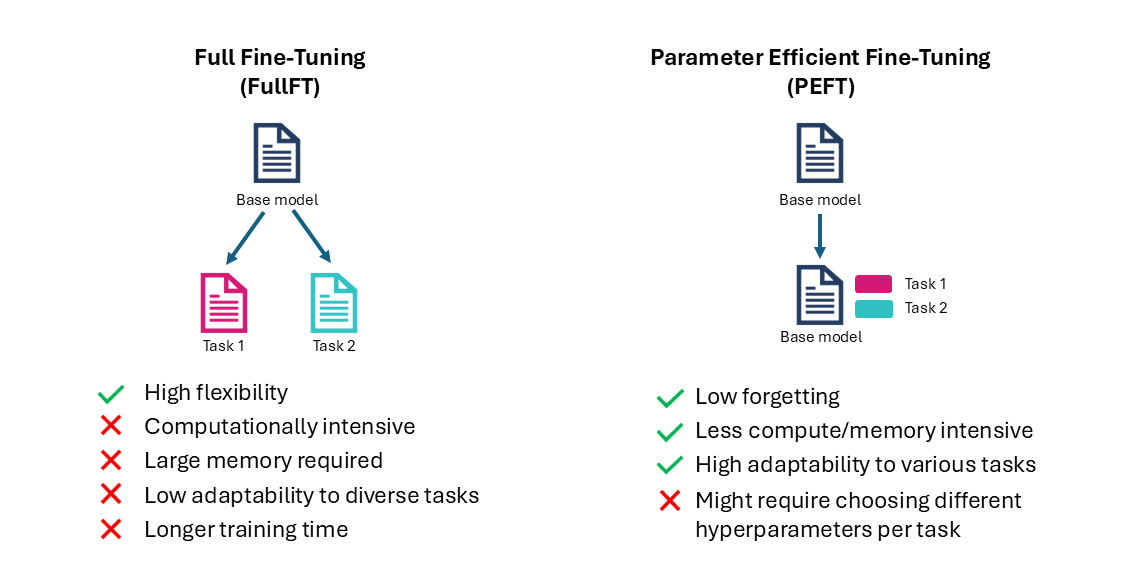
The most straightforward form of fine-tuning is defined as Full Fine-Tuning (FullFT) and it involves updating every single weight of the model. While offering high flexibility, FullFT is computationally intensive and demands significant resources.
The solution lies in Parameter Efficient Fine-Tuning (PEFT), which updates only a small set of parameters, while the others remain frozen. This approach is significantly less compute and memory instensive and it offers high adaptability across various tasks.
For instance, fine-tuning a 7B parameter model using FullFT can require up to 50GB of GPU VRAM and only 20GB using PEFT techniques (actual memory usage depends on batch size, sequence length, and specific model architecture).
LoRA: Low-Rank Adaptation Explained
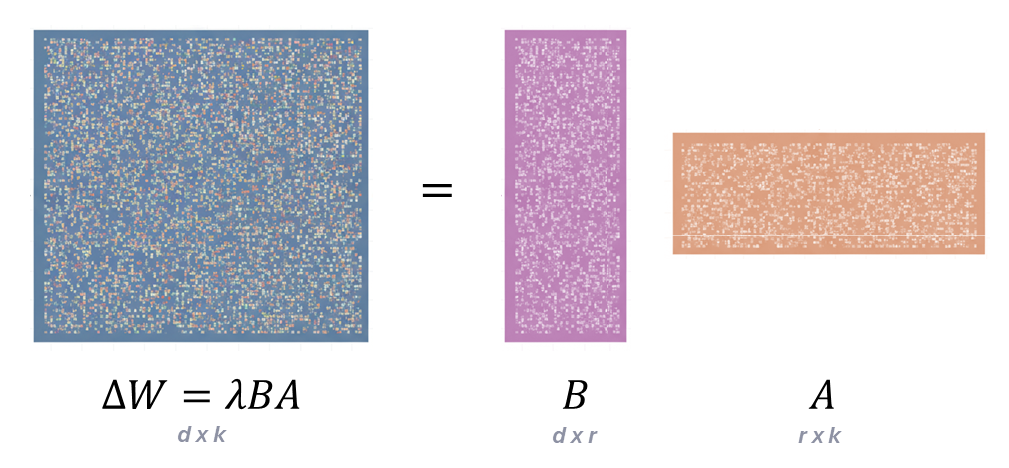
The most popular PEFT method today is LoRA, which stands for Low-Rank Adaptation. Introduced in 2021, the central idea is rooted in the hypothesis that the update required for fine-tuning a massive pre-trained weight matrix (\(W\)) has an intrinsically low rank. This means that while the original weight matrix \(W\) (which can be \(d_{model} \times d_{model}\) size) is very large, the necessary change during fine-tuning, \(\Delta W = W' - W\), (where \(W'\) is the fine-tuned weight matrix), can be effectively approximated using a technique called low-rank decomposition: \[\begin{equation*} \Delta W = \lambda BA, \text{ where }\lambda \text{ is a scaling factor}. \end{equation*}\]
Instead of learning the massive \(\Delta W\) directly, LoRA models it using two smaller trainable matrices: \(A\) (size \(d \times r\)) and \(B\) (size \(r \times k\)).
The role of rank (\(r\)) and scaling factor (\(\lambda\))
The variable \(r\) is the rank of the LoRA matrices. It is a hyperparaneter chosen by the user and it controls the number of trainable parameters. A smaller \(r\) leads to fewer parameters and greater memory savings, but a larger \(r\) generally allows the adapter to capture more complex task-specific information. Common values are between \(r=4\) to \(r=256\), based on the dataset size and the amount of new information that must be learned by the model.
The scaling factor (\(\lambda\)) control the magnitude of the weight update. It is usually defined as \(\lambda = \frac{\alpha}{r}\), where \(\alpha\) is a constant in \(r\) and it is used to prevent the scaled update from becoming too large or too small, helping stabilize the training. Tuning \(\alpha\) is roughly the same as tuning the learning rate of the optimizer, so \(\alpha\) is usually set equals to \(r\).
Where to apply LoRA
LoRA is most effective when applied to the core computational layers of the transformer architecture used in LLMs. The standard practice is to apply LoRA only to the query and value projection matrices within the self-attention layer. However, recent studies have shown that applying LoRA also to the MLP component of the feed-forward network layers can yield superior performance, sometimes rivaling FullFT.
The efficiency of LoRA
The efficiency of LoRA comes from the choice of the rank. For a weight matrix \(W\) of size \(d \times k\):
- The original number of parameters in \(W\) is \(d \times k\) (which remains frozen).
- The number of added trainable parameters by LoRA is:
\[\begin{equation*} LoRA_{params} = (d \times r) + (r \times k) ≪ d \times k \end{equation*}\]
For example, if the original \(W\) matrix is \(4096 \times 4096\) and we choose \(r=8\):
- Original parameters: \(4096 \times 4096 = 16777216\).
- LoRA parameters: \((4096 \times 8) + (8 \times 4096) = 32768 + 32768 = 65 536\), achieving a \(256\times\) reduction.
Advantages of LoRA
The benefits of using LoRA for fine-tuning are significant:
- A dramatic reduction in memory and storage requirements.
- Lower GPU VRAM consumption, enabling training on smaller hardware setups.
- Over 25% faster training compared to FullFT.
- Easy task switching by simply swapping the small LoRA adapter modules.
- No catastrophic forgetting, since the pre-trained weights remain frozen during adaptation.
LoRA vs. FullFT: Who is the winner?
While FullFT was long considered the gold standard, there is recently a lot of controversy in deciding whether LoRA can achieve similar ultimate performance and sample efficiency as FullFT.
The Illusion of Equivalence
The paper LoRA vs. full fine-tuning: An illusion of equivalence (Shuttleworth et al., 2024) challenges the idea that LoRA is truly equivalent to FullFT. The work suggests that while LoRA can match FullFT on limited budgets, achieving true equivalence requires precise optimization across all hyperparameters, and even then, in highly complex tasks, FullFT is often preferable in terms of performance. The perceived equivalence is often an illusion created by insufficient optimization of both methods or testing on limited datasets.
Learning and Forgetting Dynamics
The paper LoRA learn less and forget less (Biderman et al., 2024) explores the dynamics of knowledge transfer. It suggests that FullFT is more accurate and sample-efficient than LoRA in the majority of tasks, but LoRA forget less of the original knowledge. This property makes LoRA a safer, more stable choice for many applications, as it preserves the general capabilities of the base model while still adapting to the new task.
LoRA Without Regret
This blog post demonstrate that LoRA can indeed be on par with FullFT but only when a few key factors are chosen correctly. LoRA is most effective for post-training tasks that use small-to-medium-sized datasets, provided these datasets do not exceed LoRA’s capacity. Optimal performance is achieved when LoRA is applied broadly, including not only the attention matrices but also the MLP layers, and when a sufficiently high rank is used to capture the task’s complexity. When these best practices are followed, LoRA’s performance can approach that of FullFT.
When weighing these findings, the consensus is that it remains unclear if LoRA can match FullFT on all tasks. However, it is evident that LoRA is the recommended solution in budget-constrained scenarios. By correctly tuning the parameters and benefiting from its superior knowledge preservation, LoRA offers a powerful tool to fine-tune LLMs with a fraction of the usual cost.
Beyond LoRA
The field is rapidly innovating on top of the LoRA foundation, with new techniques further optimizing the process:
QLoRA (Quantized LoRA): This technique quantizes the large, pre-trained weights to 4-bit precision (NF4) while keeping the smaller LoRA matrices in full precision. During backpropagation the original weights are dequantized on-the-fly when needed. This approach achieves an impressive 33% GPU memory saving, at the cost of a 39% increased runtime.
DoRA (Weight Decomposed LoRA): This method decomposes the pre-trained weights into magnitude and direction. It then applies the LoRA update only to the directional component, resulting in a reported 4% accuracy improvement with minimal added parameters (0.01%).
AdaLoRA, QALoRA, etc.
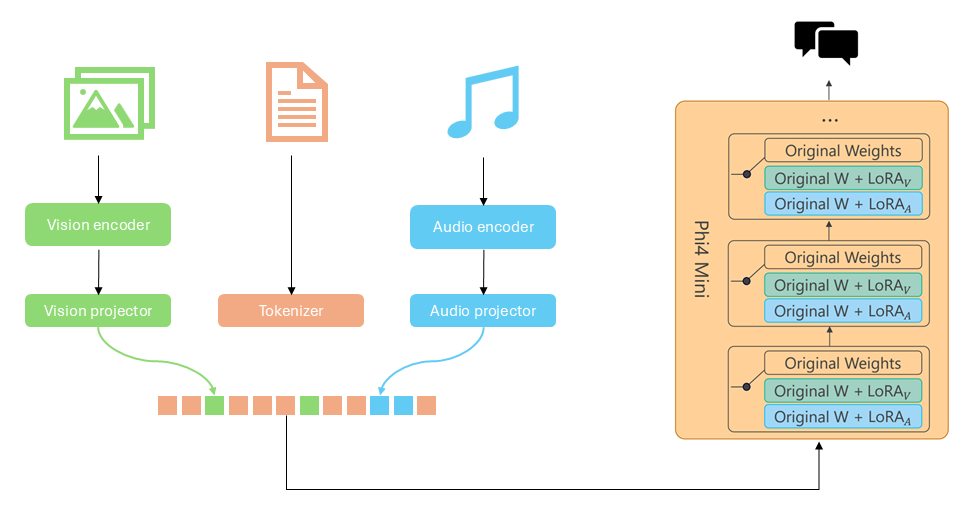
Furthermore, techniques like Mixture-of-LoRAs (MoLoRA), such as on models like Phi-4-Mini-Multimodal, use separate, dedicated LoRA adapters for different input types (e.g., for vision and for audio). This parameter-efficient strategy allows a single LLM backbone to seamlessly integrate and process complex multimodal inputs without the cost of retraining the entire system for each new modality.
Conclusion
While the general question of whether LoRA is preferable than FullFT remains open, it is clear that LoRA is a powerful and versatile fine-tuning technique. It has become the preferred approach in many applications where budget, memory efficiency, or training speed are important considerations. By carefully applying LoRA to MLP layers and selecting an appropriate rank, developers can achieve near-state-of-the-art performance at a fraction of the computational cost, making advanced LLM customization accessible to everyone.
References
- Hu, Edward J., et al. “Lora: Low-rank adaptation of large language models.” ICLR (2022).
- Dettmers, Tim, et al. “Qlora: Efficient finetuning of quantized llms.” NeurIPS (2023): 10088-10115.
- Liu, Shih-Yang, et al. “Dora: Weight-decomposed low-rank adaptation.” Forty-first International Conference on Machine Learning. 2024.
- Shuttleworth, Reece, et al. “Lora vs full fine-tuning: An illusion of equivalence.” arXiv preprint arXiv:2410.21228 (2024).
- Biderman, Dan, et al. “LoRA Learns Less and Forgets Less.” Transactions on Machine Learning Research. (2024)
- Houlsby, Neil, et al. “Parameter-efficient transfer learning for NLP.” ICML (2019).
- Abouelenin, Abdelrahman, et al. “Phi-4-mini technical report: Compact yet powerful multimodal language models via mixture-of-loras.” arXiv preprint arXiv:2503.01743 (2025).
- Schulman, John and Thinking Machines Lab, “LoRA Without Regret”, Thinking Machines Lab: Connectionism, Sep 2025.
- Practical Tips for Finetuning LLMs Using LoRA (Low-Rank Adaptation). Sebastian Raschka. 2023.
- New LLM Pre-training and Post-training Paradigms. Sebastian Raschka. 2024.
- Comparing PEFT and Full Fine-Tuning Trade-offs. ApXML.